Question

The total percent of individuals aged 16 to 24 enrolled in college as of October of each year who completed high school during the preceding 12 months is f(x)=66.925x0.044, where x is the number of years after 1999.Complete parts (a)-(c).

Answer 1

Given:

a)

`f(x)=66.925x^(0.044)`

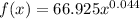
Here, x is the number of years after 1999.

For the year 2002,

`\begin{gathered} 2002-1999=3 \\ So,\text{ x=3} \\ f(x)=66.925x^(0.044) \\ f(3)=66.925(3)^(0.044) \\ =70.240\text{ percent} \end{gathered}`

For the year 2009,

`\begin{gathered} 2009-1999=10 \\ So,\text{ x=10} \\ f(x)=66.925x^(0.044) \\ f(10)=66.925(10)^(0.044) \\ =74.061 \end{gathered}`

Answer:

The total percent in 2002 is 70.240 %

The total percent in 2009 is 74.061 %.

b) The graph of the function from 2002 to 2017 is, The

c) For f(x)=100,

`\begin{gathered} f(x)=66.925x^(0.044) \\ 100=66.925x^(0.044) \\ (100)/(66.925)=x^(0.044) \\ x^(0.044)=(100)/(66.925) \\ Note\colon0.044=(11)/(250)^{} \\ (x^(0.044)_{})^{(250)/(11)}=((100)/(66.925))^{(250)/(11)} \\ x=((100)/(66.925))^{(250)/(11)} \end{gathered}`

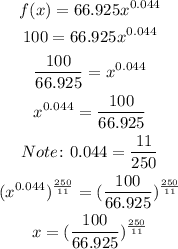
It implies that the value of x will exist for which the percentage will become 100.