Question

3, 9, 4, 4, 4, 9, 9 : Calculate the value of the sample standard deviation. Round your answer to one decimal place.

Answer 1

In order to calculate the standard deviation, we can use the following formula:

`\sigma=\sqrt[]{(\sum ^N_i(x_i-\mu)^2)/(N)}`

Where μ is the average of the sample and N is the number of elements.

So, calculating the average, we have:

`\mu=(3+9+4+4+4+9+9)/(7)=(42)/(7)=6`

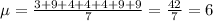
Now, using N = 7 and calculating the standard deviation, we have:

`\begin{gathered} \sigma=\sqrt[]{((3-6)^2+(9-6)^2+(4-6)^2+(4-6)^2+(4-6)^2+(9-6)^2+(9-6)^2)/(7)} \\ \sigma=\sqrt[]{(9+9+4+4+4+9+9)/(7)} \\ \sigma=\sqrt[]{(48)/(7)} \\ \sigma=2.6 \end{gathered}`

So the standard deviation is 2.6.