We have that the general rule for a dilation is:
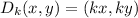
where k is the scale factor.
In this case, we have the following:
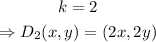
then, if we apply this transformation on points A, D and I, we have:
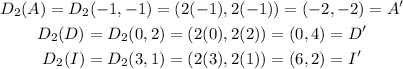
therefore, the points after the transformations are
A'=(-2,-2)
D'=(0,4)
I'=(6,2)
We have the following graph for the dilated figure:
where the green figure is the dilated figure with scale factor of 2