Based on the problem, here are the given data:
Price of the Laptop = $884.69 including tax.
Monthly Payment = $31.30
Time = 5 years = 60 months
Therefore, by the end of 5 years, Emilie will have paid $1,878.
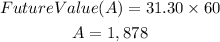
Therefore, the interest added to the original price is $993.31.
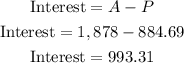
So, (assuming simple interest)
interest = 993.31
Principal = 884.69
time = 5 years
To get the interest rate, we have the formula below:
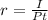
Let's substitute the values that we have to the formula above.
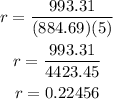
Therefore, the interest rate is 22.5%.