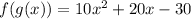Question

Express your answer as a polynomial in standard form.f(x) = 5x-15g(x) = 2x^2 + 4x – 3Find: f(g(x))

Answer 1

`f(g(x))=10x^2+20x-30`

SOLUTION

Problem Statement

The question gives us two functions f(x) and g(x) and we are required to find f(g(x)). The functions are:

`\begin{gathered} f(x)=5x-15 \\ g(x)=2x^2+4x-3 \end{gathered}`

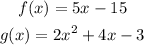
Solution

The question asks us to find f(g(x)). In f(g(x)), x has been replaced with g(x). This simply implies that wherever x is written in the expression of f(x), g(x) is used in its place.

Thus, to solve this question we simply substitute the expression of g(x) for x in the expression for f(x) to find f(g(x)).

This is done below:

`\begin{gathered} f(x)=5x-15 \\ \therefore f(g(x))=5.g(x)-15 \\ \text{ Since g(x) = }2x^2+4x-3, \\ \\ \text{Thus,} \\ f(g(x))=5(2x^2+4x-3)-15 \\ Expand\text{ the bracket, we have:} \\ f(g(x))=10x^2+20x-15-15 \\ \\ \therefore f(g(x))=10x^2+20x-30 \end{gathered}`

Final Answer

The answer is:

`f(g(x))=10x^2+20x-30`