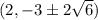Given:
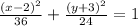
Required:
Find the endpoints of the major axis and minor axis of the ellipse.
Step-by-step explanation:
The standard equation of the ellipse is:
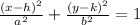
Where h and k are the centers of the ellipse and a and b are the length of the axis.
Rewrite the given equation as:

Compare the given equation with the standard equation we get
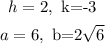
Since a>b so the coordinate x-axis will be a major axis and the y-axis will be a minor axis.
The coordinate of the major axis are:
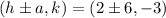
Take + sign
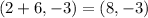
Take - sign

The coordinates of the minor axis are:
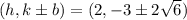
Take the + sign
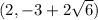
Take the - sign
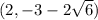
Final Answer:
The coordinates of the major axis are: (8,-3) and (-4,-3)
The coordinates of the minor axis are: