Question

A projectile is launched from the ground with an initial speed of 20 m/s at an angle of 25 degrees above the horizontal. What is the horizontal component of this projectile’s velocity the instant before it strikes the ground?

Answer 1

Given data:

* The initial speed of the projectile is u = 20 m/s.

* The angle of the projectile with the horizontal is,

`\theta=25^(\circ)_{}`

Solution:

The initial horizontal component of the speed is,

`u_x=u\cos (\theta)`

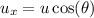
Substituting the known values,

`\begin{gathered} u_x=20\cos (25^(\circ)) \\ u_x=20*0.9063 \\ u_x=18.126\text{ m/s} \\ u_x\approx18.13\text{ m/s} \end{gathered}`

As no force acting on the projectile along the horizontal direction.

According to Newton's second law, the acceleration along the horizontal direction is,

`\begin{gathered} F=ma \\ a=(F)/(m) \\ a=0ms^(-2) \end{gathered}`

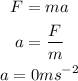
Thus, no change in the velocity takes place along the horizontal direction.

Hence, the final horizontal component of velocity before striking the ground is 18.13 m/s.