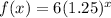The given function is:
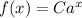
It is given that its graph passes through the points (2,9.375) and (5,18.311).
Recall that if the graph of a function passes through a point, then the coordinates of the point satisfy the equation of the function.
Substitute x=2 and f(x)=9.375 into the equation of the function:
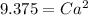
Substitute x=5 and f(x)=18.311 into the equation of the function:

Hence, the system of equation is:
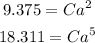
Solve the system of equations to find the constants C and a.
Divide the second equation by the first equation:
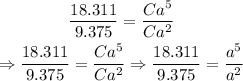
Solve for a in the equation:
![\begin{gathered} \text{Swap the sides of the equation:} \\ (a^5)/(a^2)=(18.311)/(9.375)\Rightarrow a^(5-2)=1.9532 \\ \Rightarrow a^3=1.9532 \\ \Rightarrow a=\sqrt[3]{1.9532}\approx1.25 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/fs3bqk08zagwwzpmz36hb9903cwb6danm1.png)
Substitute this value of a into the first equation to solve for C:
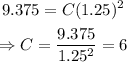
Substitute the values of a and C into the initial equation of the function:
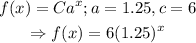
The required formula for f(x) is: