Question

The grain silo is in the shape of a cylinder the area of the circular roof is 803.84 square feet. if 13,665.28 cubic feet of grain fits in the silo, what is the radius of the silo? What is the height of the silo?

Answer 1

The grain silo has a circular roof with an area of 803.84ft²

To determine the area of a circle you have to use the following formula:

`A=\pi r^2`

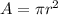
Knowing the area of the circle, you can determine the radius. The first step is to write the formula for the radius (r)

-Divide the area by pi

`(A)/(\pi)=r^2`

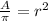
-Calculate the square root to both sides of the expression

`\begin{gathered} \sqrt[]{(A)/(\pi)}=\sqrt[]{r^2} \\ r=\sqrt[]{(A)/(\pi)} \end{gathered}`

Replace the expression with A=803.84ft²

`\begin{gathered} r=\sqrt[]{(A)/(\pi)} \\ r=\sqrt[]{(803.84)/(\pi)} \\ r=\sqrt[]{255.87} \\ r=15.995 \\ r\approx16ft \end{gathered}`

The radius of the silo is around 16ft

To determine the height of the silo you have to use the information of its volume. The volume of a cylinder can be determined using the following formula:

`V=\pi r^2h`

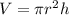
Given that we know the volume and the radius we can use this formula to determine the height, first, write the formula for h:

`\begin{gathered} V=\pi r^2h \\ h=(V)/(\pi r^2) \end{gathered}`

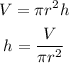
We know that V=13665.28ft³ and r=16ft, replace both values on the formula:

`\begin{gathered} h=(13665.28)/(\pi(16)^2) \\ h=(13665.28)/(256\pi) \\ h=16.99 \\ h\approx17ft \end{gathered}`

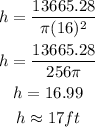
The height of the silo is 17ft