Question

May I please get help with this math problem please and figure out which figures are congruent and which are not

Answer 1

Part 1.

We can note that side AB is equal to side FD, side BC is equal to side EF and side AC is equal to side ED. Then, the triangles are congruent

By the Side-Side-Side theorem (SSS theorem)

Part 2.

In this case, we only have information about 2 quantities in each triangle: side UV and UW and YZ and XY. Then, there is no sufficient information so the triangles are not neccesarily congruent.

Part 3.

In this case, side NO is congruent to side QR, side MO is congruent to side QP and angleO is congruent to angle Q. Therefore, the triangles are congruent

`\Delta MNO\cong\Delta\text{PQR}`

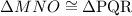
bye the side-angle-side theorem (SAS theorem)