1 Answer

Wpiwonski · Answer 1 · 2023-08-13T04:50:45+0000

We can get the exact value of a using the vertex and one point on the parabola.

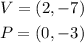
$\begin{gathered} V=(2,-7) \\ P=(0,-3) \end{gathered}$

This means h = 2, k = -7, x = 0, and y = -3. We use this value in the vertex form

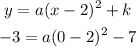
$\begin{gathered} y=a(x-2)^2+k \\ -3=a(0-2)^2-7 \end{gathered}$

Now, we solve for a

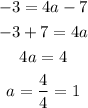
$\begin{gathered} -3=4a-7 \\ -3+7=4a \\ 4a=4 \\ a=(4)/(4)=1 \end{gathered}$

Therefore, a is equal to 1.

The image above shows the vertex point of the given parabola. Also shows the point we used.