Question

After being rejected for employment, Kim Kelly learns that the Bellevue Credit Company has hired only four women among the last 22 new employees. She also learns that the pool of applicants is very large, with an approximately equal number of qualified men as qualified women.Help her address the charge of gender discrimination by finding the probability of getting four or fewer women when 22 people are hired, assuming that there is no discrimination based on gender.(Report answer accurate to 8 decimal places).P(at most four)

Answer 1

Given:

The number of employee=22

The probability of selecting women is 1/2. As there are equal number of qualified men as qualified women.

The data follows binomial distribution,

`\begin{gathered} X\text{ \textasciitilde{}B(n,p,q)} \\ n=22 \\ p=(1)/(2)=0.5 \\ q=1-p=1-0.5=0.5 \\ P(X=x)=^nC_xp^xq^(n-x) \end{gathered}`

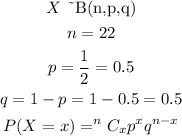
The probability that four or fewer women are selected for 22 positions is,

Answer: P( at most four ) = 0.00217175 (nearest to 8 decimal places)