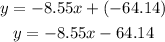Question

What is an equation of the line of best fit?

Answer 1

To begin we shall determine the mean of both the x values and the y values as follows;

`\begin{gathered} \bar{X}=(10.2+10.4+10.5+10.5+10.5+10.6+10.8+10.8+10.9+11+11.2)/(11) \\ \bar{X}=(117.4)/(11) \\ \bar{}X=10.67 \\ \bar{Y}=(31+27+29+30+31+26+25+26+27+24+22)/(11) \\ \bar{Y}=(298)/(11) \\ \bar{Y}=27.09 \end{gathered}`

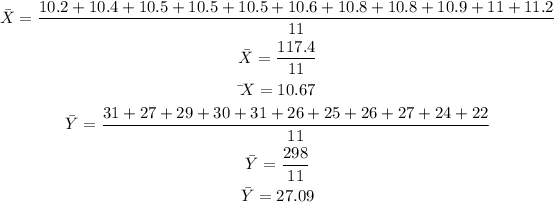
The mean of the x values is 10.67 while the mean of the y values is 27.09.

Next we c alculate x minus mean of x for every single x value, and do the same for the y values. This is shown below;

`\begin{gathered} (x_1-\bar{X})=-0.47 \\ (x_2-\bar{X})=-0.27 \\ (x_3-\bar{X})=-0.17 \\ (x_4-\bar{X})=-0.17 \\ (x_5-\bar{X})=-0.17 \\ (x_6-\bar{X})=-0.07 \\ (x_7-\bar{X})=0.13 \\ (x_8-\bar{X})=0.13 \\ (x_9-\bar{X})=0.23 \\ (x_(10)-\bar{X})=0.33 \\ (x_(11)-\bar{X})=0.53 \end{gathered}`

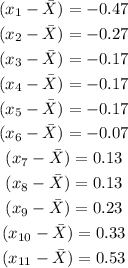
We do the same for the y values as shown below;

`\begin{gathered} (y_1-\bar{Y})=3.91 \\ (y_2-\bar{Y})=-0.09 \\ (y_3-\bar{Y})=1.91 \\ (y_4-\bar{Y})=2.91 \\ (y_5-\bar{Y})=3.91 \\ (y_6-\bar{Y})=-1.09 \\ (y_7-\bar{Y})=-2.09 \\ (y_8-\bar{Y})=-1.09 \\ (y_9-\bar{Y)=-0.09} \\ (y_(10)-\bar{Y})=-3.09 \\ (y_(11)-\bar{Y})=-5.09 \end{gathered}`

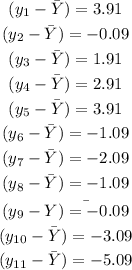
Next step is to multiply each value derived above line by line as follows;

`\begin{gathered} (x_i-\bar{X})*(y_i-\bar{Y}) \\ H\text{ence:} \\ (x_1-\bar{X})(y_1-\bar{Y}),(x_2-\bar{X})(y_2-\bar{Y})\ldots \\ \text{And so on till we get to the 11th term} \end{gathered}`

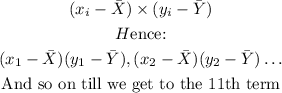
We would now have;

`\begin{gathered} (x_1-X)(y_1-Y)=-1.8377 \\ (x_2-X)(y_2-Y)=0.0243 \\ (x_3-X)(y_3-Y)=-0.3247_{} \\ (x_4-X)(y_4-Y)=-0.4947 \\ (x_5-X)(y_5-Y)=-0.6647 \\ (x_6-X)(y_6-Y)=0.0763 \\ (x_7-X)(y_7-Y)=-0.2717 \\ (x_8-X)(y_8-Y)=-0.1417 \\ (x_9-X)(y_9-Y)=-0.0207 \\ (x_(10)-X)(y_(10)-Y)=-1.0197 \\ (x_(11)-X)(y_(11)-Y)=-2.6977 \end{gathered}`

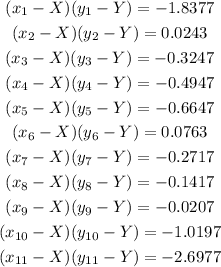
We sum this all together to arrive at;

`(x_1-X)(y_1-Y)+(x_2-X)(y_2-Y)+\cdots(x_(11)-X)(y_(11)-Y)=-7.3727`

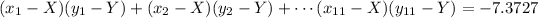
Next step we square and add up all 11 terms of the x values minus the mean of x, as follows;

`\begin{gathered} (x_1-X)^2+(x_2-X)^2+\cdots(x_(11)-X)^2=0.8619 \\ \end{gathered}`

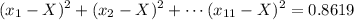
We can now calculate the slope which is given by the formula;

`\begin{gathered} m=(\Sigma(x_i-X)(y_i-Y))/(\Sigma(x_i-X)^2)=(-7.3727)/(0.8619) \\ m=-8.55400 \\ m\approx-8.55 \end{gathered}`

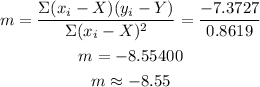
We can now insert these values into the equation in slope-intercept form in order to derive the y-intercept as follows;

`\begin{gathered} y=mx+b \\ Where; \\ x=\bar{X},y=\bar{Y} \\ y=mx+b\text{ now becomes} \\ 27.09=-8.55(10.67)+b \\ 27.09=91.2285+b \\ 27.09-91.2285=b \\ b=-64.1385 \\ b\approx-64.14 \end{gathered}`

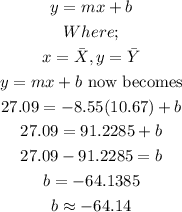
ANSWER:

The equation that gives the line line of best fit therefore is;

`\begin{gathered} y=-8.55x+(-64.14) \\ y=-8.55x-64.14 \end{gathered}`