Given the following vectors:

We will find the following:
a) -7u • v
The dot product of two vectors will be as follows:
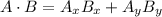
So, for the given product, the answer will be as follows:
![\begin{gathered} -7u\cdot v=-7(-4)(8)(\cos 60\cdot\cos 135+\sin 60\cdot\sin 135) \\ =224((1)/(2)\cdot(-\frac{1}{\sqrt[]{2}})+\frac{\sqrt[]{3}}{2}\cdot\frac{1}{\sqrt[]{2}}) \\ \\ =224(-\frac{1}{2\sqrt[]{2}}+\frac{\sqrt[]{3}}{2\sqrt[]{2}})\cdot\frac{\sqrt[]{2}}{\sqrt[]{2}} \\ \\ =224(-\frac{\sqrt[]{2}}{4}+\frac{\sqrt[]{6}}{4})=56(\sqrt[]{6}-\sqrt[]{2}) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/4ru8gmw4w21uotr04mpz9mrgn29io35650.png)
Part B: Use the dot product to determine if u and w are parallel, orthogonal, or neither
The vectors will be parallel if the dot product = the product of the magnitudes which means the angle between the vectors = 0 or 180
And the vectors will be orthogonal of the dot product = 0
This means the angle between them = 90
The dot product of the vectors (u) and (w) will be as follows:
![\begin{gathered} u\cdot w=(-4)(12)(\cos 60\cos 150+\sin 60\sin 150) \\ =(-48)((1)/(2)\cdot\frac{-\sqrt[]{3}}{2}+\frac{\sqrt[]{3}}{2}\cdot(1)/(2)) \\ \\ =(-48)(\frac{-\sqrt[]{3}}{4}+\frac{\sqrt[]{3}}{4})=(-48)(0)=0 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/2tpt0tyal1i0vdkft1d46gpn4l531ht7rx.png)
So, as the result of the dot product = 0
The vectors (u) and (w) are Orthogonal.