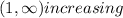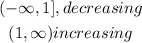
1) In this question, we need to remind ourselves of the definition of an increasing or decreasing interval.
2) When the function is increasing we have:
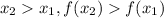
On the other hand, a given interval of a function is decreasing when:
![x_2>x_1,f(x_2)<strong>3) </strong>Examining the graph we see two intervals:[tex]\begin{gathered} (-\infty,1\rbrack \\ (1,\infty) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/d2oo1mapw5lv0jdaztfgu2qp69wpf1ark9.png)
Note that for the first interval the more the f(x) values increase the x values decrease.
So,
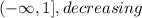
And on the other hand, the more the x values increase the more the f(x) values increase, so: