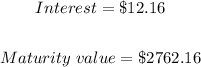Question

1. Ryan is taking out a short-term loan of $2,750 for 35 days. If the loan has an ordinary interest rate of4.55%, find the interest he pays and also the loan's maturity value.

Answer 1

GIVEN:

We are told that Ryan is taking a short term loan of $2750 for 35 days.

The ordinary interest rate is 4.55%.

Required;

To find the interest he pays

The Loan's maturity value

Step-by-step solution;

To calculate the simple interest on a loan the formula is;

`I=P* R* T`

Where the variable T is given in years. However, when the loan is taken for a period less than a year, then the variable T becomes number of days given divided by 360, assuming a 360-day year.

`\begin{gathered} I=interest \\ P=principal(2750) \\ R=annual\text{ }rate(0.0455) \\ T=(35)/(360) \end{gathered}`

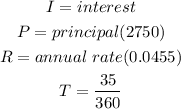
We can now calculate the interest he pays as follows;

`\begin{gathered} I=2750*0.0455*(35)/(360) \\ \\ I=12.1649305556 \end{gathered}`

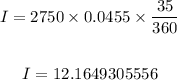
Rounded to the nearest cent, we now have,

`I\approx12.16`

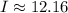
The loan's maturity value is the addition of the principal amount and the amount of interest and that is;

`\begin{gathered} A=P+I \\ \\ A=2750+12.16 \\ \\ A=2762.16 \end{gathered}`

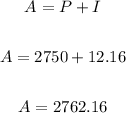
Therefore,

ANSWER:

`\begin{gathered} Interest=\text{\$}12.16 \\ \\ Maturity\text{ }value=\text{\$}2762.16 \end{gathered}`