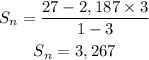Question

Show all work to determine thesum of this following series.9Σ 3-2x=5Please show all work

Answer 1

we have the expression

`\sum_{x\mathop{=}5}^93^((x-2))=3^((5-2))+3^((6-2))+3^((7-2))+3^((8-2))+3^((9-2))`
`\begin{gathered} =3^3+3^4+3^5+3^6+3^7 \\ =27+81+243+729+2,187 \\ =3,267 \end{gathered}`

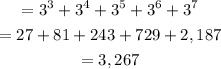
the answer is 3,267

Another way

we have the formula

`S_n=(a_1-a_n*r)/(1-r)`

where

For x=5

a1=3^(5-2)=27

For x=9

a5=3^(9-2)=2,187

r=3

substitute the given values in the formula

`\begin{gathered} S_n=(27-2,187*3)/(1-3) \\ \\ S_n=3,267 \end{gathered}`

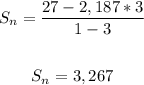
The answer is 3,267

Step-by-step explanation

we have the formula

`S_(n)=(a_(1)-a_(n)r)/(1-r)`

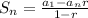
step 1

Find out the first term a1

a1=3^(x-2)

the first term is for x=5

a1=3^(5-2)=3^3=27

step 2

Find out the last term

an=3^(x-2)

For x=9

an=3^(9-2)=3^7=2,187

step 3

In the formula, the value of r (common ratio in geometric series) is equal to

r=3

step 3

Substitute the given values in step 1 and step 2 in the formula

`\begin{gathered} S_(n)=(27-2,187*3)/(1-3) \\ S_(n)=3,267 \end{gathered}`