Question

Hi, can you help me with this question, please, thank you:)

Answer 1

P(at least one defective) = 0.0873 (4 decimal places)

STEP BY STEP EXPLANATION

Given that a 3% defect rate = p = 3/100 = 0.03

Now, 3 items are chosen at random

Probability that no one will have a defect = P(0)

Let's use Binomial Distribution to determine the P(0)

`P(x)=^nC_xp^x(1-p)^(n-x)`

`\begin{gathered} P(0)=^3C_0(0.03)^0(1-0.03)^(3-0) \\ \text{ = 1}*1*(0.97)^3 \\ \text{ = 0.912673} \end{gathered}`

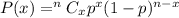
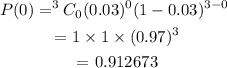
Now, Probability of at least one will have a defect:

`\begin{gathered} P(x\ge1)\text{ = 1 - P(0)} \\ \text{ = 1 - 0.912673} \\ \text{ = 0.087327} \end{gathered}`

Hence, the probability that one will have a defect is 0.0873 (4d.p)