Question

Hey, I was wondering if you could help me with this problem, I understand how to do these types of problems but this particular question confused me.

Answer 1

Given:

The point C is (-1,7) and the point D is (5,1).

To point that partitions CD in the ratio 3:1 is gotten using the formula;

where;

`\begin{gathered} a=3,b=1 \\ x_1=-1,y_1=7 \\ x_2=5,y_2=1 \end{gathered}`

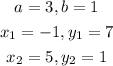
Substituting these values into the equation;

`\begin{gathered} (x,y)=((1(-1)+3(5))/(1+3),(1(7)+3(1))/(1+3)) \\ (x,y)=((-1+15)/(4),(7+3)/(4)) \\ (x,y)=((14)/(4),(10)/(4)) \\ (x,y)=(3.5,2.5) \end{gathered}`

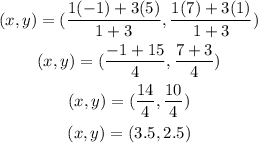
Therefore, the point that partitions the line segment CD in the ratio 3:1 is (3.5,2.5)