If we have that the square room has a floor area of 36ft², we can calculate the side of each of the sides of the floor. After finding the measure of the side, then we can calculate the area of one of the walls. Finally, we have to multiply this result by 4 to obtain the total area of the walls.
We can proceed as follows:
Finding the measure of the side of the square floor
We have that the square room has an area of 36ft². Then we have:
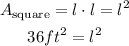
Then if we take the square root to both sides of the equation:
![\begin{gathered} l^2=36ft^2 \\ \sqrt[]{l^2}=\sqrt[]{36ft^2} \\ l=6ft \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/zxk8esiyli92cgbfj5a1koiova54ueu5dq.png)
Therefore, each side of the floor measures 6ft.
Finding the area of the walls
Since we know that the height of the walls is 7ft, we can find the area of one wall as follows:

We calculated for the area of a rectangle.
Since we have four walls, then the total area of all four walls will be:
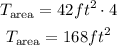
In summary, therefore, the total area of all four walls is 168ft² (168 square feet).