Answer:
5.952
Step-by-step explanation:
First, we need to find the mean of the data. So, the sum of all the values divided by the number of values is equal to:
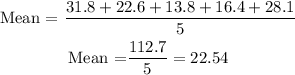
Then, we need to find the absolute difference between each value and the mean, so:
| 31.8 - 22.54 | = 9.26
|22.6 - 22.54 | = 0.06
|13.8 - 22.54 | = 8.74
| 16.4 - 22.54 | = 6.14
| 28.1 - 22.54| = 5.56
Finally, sum the differences and divide them by the number of values:

Therefore, the mean absolute deviation is 5.952