The form of the quadratic function is

Where c is the y-intercept, value y at x = 0
From the given picture
There are 3 points lie on f(x) (0, 3), (1, 2), (3, -12)
Since at x = 0, y = 3, then
The y-intercept is (0, 3), then
c = 3
The function could be A, or C, or D
Then we will use the point (1, 2) to find which of them is the answer
Substitute x by 1 in equation A to find f(x) (value of y)
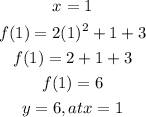
But at x = 1, y = 2
Then A is wrong
Substitute x by 1 in equation C
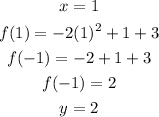
Since the value of y equal the y-coordinate at x = 1
Then C is correct
The function that contains points (0, 3), (1, 2), and (3, -12) is C