Question

For the point P(-3,0) and Q(4,3), find the distance d(P,Q) and the coordinates ofthe midpoint M of the segment PQ.

Answer 1

Write out the given coordinate of point P and Q

`\begin{gathered} P=(-3,0) \\ \text{and} \\ Q=(4,3) \end{gathered}`

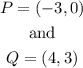
The distance between two point is given by

`\text{dist}=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}^{}`

Given point P(-3,0) and Q(4,3)

`\begin{gathered} x_2=4,x_1=-3,y_2=3,y_1=0 \\ \text{Then } \\ \text{dist(P,Q)}=\sqrt[]{(4-(-3)^2+(3-0)^2} \end{gathered}`

Hence, by simplification, we have

`\begin{gathered} \text{dist(P,Q)}=\sqrt[]{7^2+3^2}=\sqrt[]{49+9}=\sqrt[]{58} \\ \end{gathered}`

Hence

The distance between point P and Q is √58 unit

Then

The coordinates of the midpoint is given by

`\begin{gathered} Let\text{ the coordinate of the midpoint m be } \\ (x_m,y_m) \\ \text{Hence } \\ (x_m,y_m)=((x_1+x_2)/(2)+(y_1+y_2)/(2)) \end{gathered}`

Where

`\begin{gathered} x_2=4,x_1=-3,y_2=3,y_1=0 \\ \text{Then} \\ (x_m,y_m)=((-3+4)/(2),(3+0)/(2)) \\ \\ (x_m,y_m)=((1)/(2),(3)/(2)) \end{gathered}`

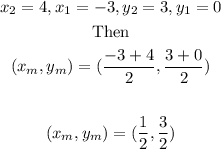
Therefore

The coordinates of the midpoint M of the segment PQ is (1/2,3/2)