The efficiency of a car is the measure of how far can it travel in one liter of gas.
Thus the efficiency can be calculated as,
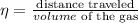
a. Given, the car traveled for d=80 km in V=5.0 L of gas.
Thus the efficiency in this case is,
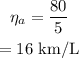
b.
Given, the car traveled for 90 km using 6.0 L of gas
Thus the efficiency in this case is,

c.
Given, the car travels for 50 km on 4.0 L of gas.
Thus the efficiency of the car, in this case, is given by,
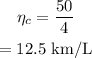
d.
Given,
The car travels for a distance of 70 km using 5.0 L of gas.
Therefore, the efficiency of the car, in this case, is given by,

Thus on comparing, the car in the option a achieved the greatest efficiency.
Therefore, the correct answer is option a.