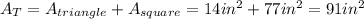Question

Find the Area 11 in 7 in 8.1 in 15 in

Answer 1

`A_T=91in^2`

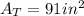
Step-by-step explanation: We need to find the area of the given object, and as it can be seen that it can be thought of as composed of a square and a triangle, so if we could decompose it into a square and triangle and then find the area of these two shapes individually, then the final answer would be the sum of these two individual areas:

Area of Square:

A square can be extracted out of this image and it would have the dimensions of:

`\begin{gathered} h=7\text{ in} \\ w=11\text{ in } \end{gathered}`

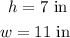
And therefore the area would be:

`\begin{gathered} A_(square)=h* w=7in*11in=77in^2 \\ A_(square)=77in^2 \end{gathered}`

Area of Triangle:

Similarly, a triangle can be extracted from the overall shape, which has the dimensions of:

`\begin{gathered} h=7in \\ b=(15-11)\text{ in=4in} \end{gathered}`

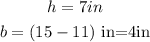
Similarly, the area would be:

`\begin{gathered} A_(triangle)=(1)/(2)(h* b)=(1)/(2)(7in*4in)=(28)/(2)in^2=14in^2 \\ A_(triangle)=14in^2 \end{gathered}`

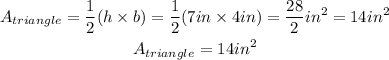
Finally, the total area would be:

`A_T=A_(triangle)+A_(square)=14in^2+77in^2=91in^2`