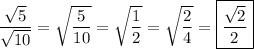Question

Rationalise the denominator and simplify

Answer 1

a) 2

b) (√2)/2

Explanation:

You want to rationalize the denominator and simplify the expressions (√12)/(√3) and (√5)/(√10).

There are a couple of ways to approach this. The straightforward "rationalize the denominator" requires that you multiply numerator and denominator by the root in the denominator. Then, any squares under the radical in the numerator can be removed.

Alternatively, the ratio of roots can be written as the root of a ratio, which can be rewritten as a ratio with a perfect square denominator. Then taking the root is gets you the simplified form of the expression.

a)

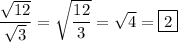
`(√(12))/(√(3))=\sqrt{(12)/(3)}=√(4)=\boxed{2}`

b)

`(√(5))/(√(10))=\sqrt{(5)/(10)}=\sqrt{(1)/(2)}=\sqrt{(2)/(4)}=\boxed{(√(2))/(2)}`