We are given the following function which models the leakage of water from a tank.
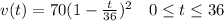
Where v(t) is the amount of water left after t minutes, and t is the time in minutes.
70 gallons is the initial water in the tank and the tank gets empty after 36 minutes.
(a) v(0) and v(36)
Let us substitute t = 0 into the function
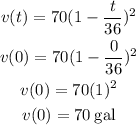
So, this means that when t is equal to 0 minutes then the amount of water in the tank is 70 gallons.
Now, let us substitute t = 36 into the function
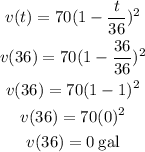
So, this means that when t is equal to 36 minutes then the amount of water in the tank is 0 gallons.
(b)
v(0) = 70 gallons represents the initial volume of the tank.
v(36) = 0 gallons represents the final volume of the tank.
Therefore, the correct answer is the last option.
v(0) represents the initial volume, and v(36) represents the final volume.
(c)
Let us substitute t = 0, 9, 18, 27, 36 into the function and find the corresponding volume v(t)
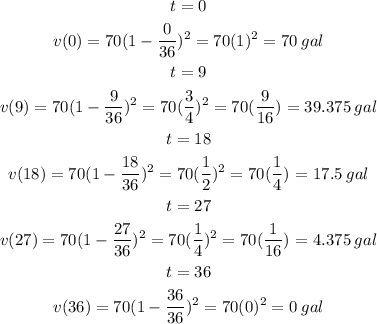
Therefore, the table of values is
(d) The net change in the volume is given by
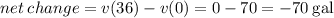
Therefore, the net change in the volume is -70 gallons
The negative sign is due to the fact that overall, the volume has decreased in the tank.