For this exercise you need to remember that, when two parallel lines are cut by a transversal, one of the pair of angles formed is the following: Interior angles on the same side of the transversal.
The angles mentioned above are Supplementary when the lines are parallel.
Supplementary angles are defined as those angles that add up to 180 degrees.
Based on the explained above, you can set up the following equation for this case:
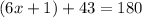
Finally, solve for "x" in order to find its value. This is:
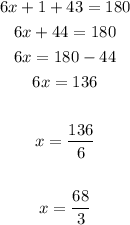
In order to convert the Improper fraction to Mixed number, you need to follow these steps:
- Divide the numerator 68 by the denominator 3.
- The Quotient 22 will be the Whole number.
- The Remainder 2 will be the new numerator.
- The denominator is the same: 3.
Then:
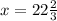
The answer is: Option 3.