To find the derivative of
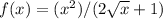 using the Quotient Rule, calculate the derivatives of the numerator and the denominator separately, then apply the rule to obtain the derivative of the function.
using the Quotient Rule, calculate the derivatives of the numerator and the denominator separately, then apply the rule to obtain the derivative of the function.
Step-by-step explanation:
Using the Quotient Rule to find the derivative of the function
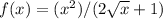 , we need to define the numerator as
, we need to define the numerator as
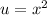 and the denominator as
and the denominator as
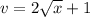 . The Quotient Rule states that the derivative of a function in the form of u/v is given by
. The Quotient Rule states that the derivative of a function in the form of u/v is given by
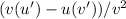 . So, calculate the derivatives u' = 2x and
. So, calculate the derivatives u' = 2x and
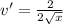 (using the chain rule and power rule for v'). Substituting these into the Quotient Rule formula gives the derivative of the function.
(using the chain rule and power rule for v'). Substituting these into the Quotient Rule formula gives the derivative of the function.
Firstly,
u' = 2x
Secondly,
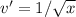
Thus, the derivative of f(x) becomes:
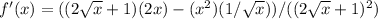 . This simplifies to give the final expression for the derivative after combining like terms and simplifying the fraction.
. This simplifies to give the final expression for the derivative after combining like terms and simplifying the fraction.