Answer:
S' = (-4, -10)
T' = (-4, 0)
U' = (3, 0)
V = (3, -10)
Step-by-step explanation:
Given:
quadrilateral STUV
To find:
The coordinates of the vertex when it is translated 7 units to the left and 7 units down
To determine the new coordinates, we wil be apply int theranslation rlule:

Initial coordinates of the vertx:
S = (3, -3), T = (3, 7), U = (10, 7) and V = (10, -3)
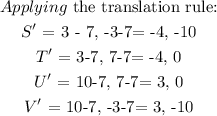
S' = (-4, -10)
T' = (-4, 0)
U' = (3, 0)
V = (3, -10)