Question

7. If QT is the perpendicular bisector of PR, find each measure.Sy - 31-PQ =OR =PS7x - 17SR -PTPR -

Answer 1

Given QT is perpendciular bisector of PR.

So, PT=TR=6x-2y.

Given, PQ=5y-31, QR=2y+5.

Using Pythagoras theorem in triangle PQT,

`\begin{gathered} \text{Hypotenuse}^2=Base^2+Altitude^2 \\ Altitude^2=\text{Hypotenuse}^2-Base^2 \\ QT^2=PQ^2-PT^2\ldots\ldots.(1) \end{gathered}`

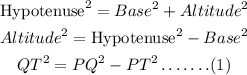
Using Pythagoras theorem in triangle QRT,

`\begin{gathered} \text{Hypotenuse}^2=Base^2+Altitude^2 \\ Altitude^2=\text{Hypotenuse}^2-Base^2 \\ QT^2=QR^2-TR^2\ldots\ldots.(2) \end{gathered}`

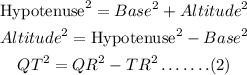
Equate equations (1) and (2).

`PQ^2-PT^2=QR^2-TR^2`

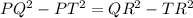
Since PT=TR, we can write

`\begin{gathered} PQ^2-PT^2=QR^2-PT^2 \\ PQ^2=QR^2 \\ PQ=QR \\ 5y-31=2y+5 \\ 5y-2y=5+31 \\ 3y=36 \\ y=(36)/(3)=12 \end{gathered}`

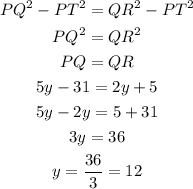
Now, put y=12 in PQ=5y-31.

`PQ=5*12-31=29`

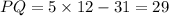
Since PQ=QR, QR=29.

Given, PS=4x+4, SR=7x-17.

Also, PS=SR. Hence,

`\begin{gathered} 4x+4=7x-17 \\ 4+17=7x-4x \\ 21=3x \\ (21)/(3)=x \\ 7=x \end{gathered}`

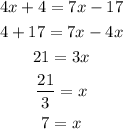
Put x=7 and y=12 in PT=6x-2y to find PT.

`PT=6*7-2*12=18`

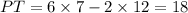
Hence, PT=18.

Since PT=TR, PR=2PT.

Therefore,

`\begin{gathered} PR=2PT \\ =2*18=36 \end{gathered}`

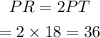
Put x=7 in PS=4x+4 .

`PS=4*7+4=32`

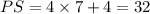
Since PS=SR, SR=32.

Therefore,

x=7

y=12

PQ=29

QR=29

PS=32

SR=32

PT=18

PR=36