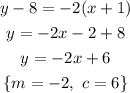Question

graph and label the lines given the equation in point slope form. Convert to slope intercept to graph.y-2=3/4(x+5)y+4= -5/2(x-6)y-8= -2(x+1)

Answer 1

The general point slope form of a line is given as;

`y-y_1=m(x-x_1_{})`

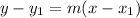
From the 1st given equation, we can deduce that;

`y_1=2,m=(3)/(4),x_1=-5`

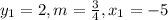
From the 2nd equation, we can deduce that;

`y_1=-4,m=-(5)/(2),x_1=6`

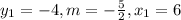
From the 3rd equation, we can deduce that;

`y_1=8,m=-2,x=-1`

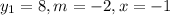
Let's go ahead and graph the lines;

Let's convert each of the given equations to a slope intercept form equation;

Remember, that the equation in a slope intercept form is always given as;

`\begin{gathered} y=mx+c \\ \text{Where m is the slope and c is the intercept} \end{gathered}`

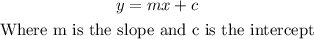
So, converting the 1st equation into the slope intercept form, we'll have;

`\begin{gathered} y-2=(3)/(4)(x+5) \\ 4y-8=3x+15 \\ 4y=3x+23 \\ y=(3)/(4)x+(23)/(4) \\ y=0.75x+5.75 \\ \lbrace m=0.75,c=5.75\} \end{gathered}`

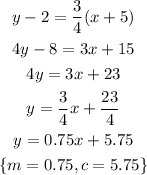
Let's go ahead and convert the 2nd equation;

`\begin{gathered} y+4=-(5)/(2)(x-6) \\ 2y+8=-5x+30 \\ y=-(5)/(2)x+11 \\ y=-2.5x+11 \\ \lbrace m=-2.5,c=11\rbrace \end{gathered}`

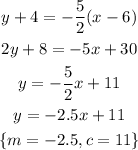
Let's convert the 3rd equation;

`\begin{gathered} y-8=-2(x+1) \\ y=-2x-2+8 \\ y=-2x+6 \\ \lbrace m=-2,\text{ }c=6\rbrace \end{gathered}`