Given that Mrs Robinson's class, 19 basic yearbooks and 4 deluxe yearbooks were ordered, for a total of $1,841.
Also, Mr Yamamoto's class ordered 19 basic yearbooks and 16 deluxe yearbooks, for a total of $2,861.
Suppose that the basic yearbook is denoted by x and deluxe yearbooks is denoted by y then Mrs Robinson's purchase can be written in the equation as follows,
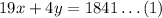
Also, Mr Yamamoto's purchase can be written in the equation as follows,
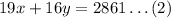
Next, substract equation (2) from equation (1) as follows,
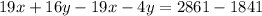
Further, solve the obtained result as follows,
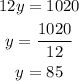
As a result, obtained that y is equal to 85.
Furthermore, substitute y = 85 in equation (1) as follows,
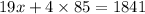
Further, solve the obtained result as follows,
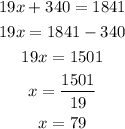
As a result, obtained that the value of x is equal to 79.
Thus, the required value of the basic yearbook is 79 and the deluxe yearbook is 85.