Given:
The mass of the base runner is: m = 63 kg
The initial speed of the base runner is: u = 4.3 m/s
The coefficient of friction is: μ = 0.70
To find:
a) The amount of mechanical energy lost due to friction
b) How far the base runner slides?
Step-by-step explanation:
We use the work-energy theorem to determine the loss in the mechanical energy of the base runner. Thus, we get:
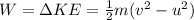
Here, v is the final velocity of the base runner which is zero. Thus, v = 0 m/s.
Substituting the values in the above equation, we get:
![\begin{gathered} W=\Delta KE=(1)/(2)*63\text{ kg}*[(0\text{ m/s})^2-(4.3\text{ m/s})^2] \\ \\ W=\Delta KE=(1)/(2)*63\text{ kg}*[-18.49\text{ m}^2\text{/s}^2] \\ \\ W=\Delta KE=-582.435\text{ J} \\ \\ W=\Delta KE\approx-582.44\text{ J} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/1ju9tdbob53cnxfrtkaz4wjhmn0a0bddly.png)
The negative sign indicates energy lost in due to friction. Thus, the mechanical energy lost due to friction is 582.44 Joules.
The negative sign also indicates frictional force is acting in the opposite direction of the displacement of the base runner.
As the frictional force is opposite to the displacement of the base runner, the angle between the displacement direction and the frictional force is 180°. Thus, the work done by the frictional force is calculated as:
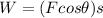
Here, s is the displacement of the base runner.
Rearranging the above equation, we get:
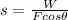
The frictional force F can be expressed as:
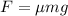
Thus, the equation of displacement "s" can be written as"
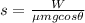
Substituting the values in the above equation, we get:

Final answer:
a) The loss in mechanical energy due to friction is 582.44 Joules.
b) The base runner covers a distance of 1.35 m by sliding.