In this problem, we have a triangle with sides:
• PR = 4x,,
,
• RQ = x + 3,
,
• QP = 5x - 1,
,
• and perimeter p = 72.
By definition, the perimeter is the sum of the length of the sides, so we have:
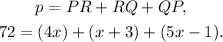
Solving for x the last equation, we find that:
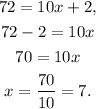
Replacing the value x = 7 in the equation of side PR, we have:
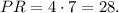
Answer
PR = 28