Question

List the operations being applied and the order in which they are applied to the variable. Choose the correct answer below.

Answer 1

Given:

`3y^3-4`

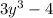
This expression can be written as follows.

Cube the variable, multiply by 3, and then subtract 4.

Take the given expression as x as follows to find the inverse.

`3y^3-4=x`

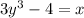
Adding 4 on both sides of the equation, we get

`3y^3-4+4=x+4`

`3y^3=x+4`

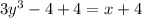
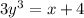
Dividing both sides by 3, we get

`(3y^3)/(3)=(x+4)/(3)`

`y^3=(x+4)/(3)`

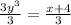
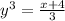
Taking cube root on both sides, we get

`y=\sqrt[3]{(x+4)/(3)}`

Hence the inverse expression is

`\sqrt[3]{(x+4)/(3)}`

This can be written as follows.

Add 4, divide by 3 and then take the cube root of the variables.