Given:
Mass, m = 1.4 kg
Spring constant, k = 140 N/m
x1 = 0.12 m
Let's find the speed of the block when the elongation is x = 0.06 m
Apply the Conservation of Energy formula:
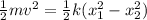
Since we are to find the speed, rewrite the formula for v:
![v=\sqrt[]{(k(x^2_1-x^2_2))/(m)}](https://img.qammunity.org/2023/formulas/physics/college/rjwupg1wjjn2wkgrzoqzlraaf57q4t3uv4.png)
Where:
k = 140 N/m
x1 = 0.12 m
x2 = 0.06 m
m = 1.4 kg
Hence, we have:
![\begin{gathered} v=\sqrt[]{(140(0.12^2-0.06^2))/(1.4)} \\ \\ v=\sqrt[]{(1.512)/(1.4)} \\ \\ v=1.039\text{ m/s} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/z29d6w0ddmqwrsfbtiz9m68c3gyrgpp7nc.png)
Therefore, the speed of the block when the elongation is x=0.06m is = 1.039 m/s.
ANSWER:
1.039 m/s