Question

There are eight black balls and eight red balls in an urn. If 5 balls are drawn without replacement what is the probability that exactly 3 blackballs are drawn express your answer as a fraction or decimal number rounded to four decimal places

Answer 1

Given:

The number of black balls = 8.

The number of red balls = 8.

Five balls are drawn without replacement.

Required:

We need to find the probability that exactly 3 blackballs are drawn.

Step-by-step explanation:

The total number of balls in an urn =8+8 = 16 balls.

The total number of selections of 5 balls of which three are black balls are drawn.

`=3\text{ black balls and 2 red balls}`
`=8C_3*8C_2`
`=(8!)/(3!(8-3)!)*(8!)/(2!(8-2)!)`

`=(8!)/(3!*5!)*(8!)/(2!*6!)`
`=(8*7*6*5!)/(3*2*5!)*(8*7*6!)/(2*6!)`
`=8*7*4*7`
`=1568`

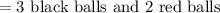
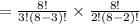
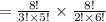
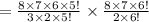
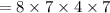
All possible out for drawing 5 balls is

`=16C_5`
`=(16!)/(5!(16-5)!)`
`=(16*15*14*13*12*11!)/(5*4*3*2*11!)`
`=16*3*7*13`
`=4368`

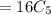
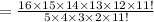
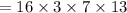
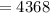
The probability that exactly 3 blackballs are drawn is

`P(exactly\text{ 3\rparen=}(1568)/(4368)`

`P(exactly\text{ 3\rparen=0.3590}`

Final answer:

`P(exactly\text{ 3\rparen=0.3590}`