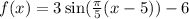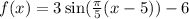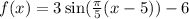Question

Write the formula of the function, where x is entered in radians.

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Write the general form of a sinusoidal function

`\begin{gathered} f(x)=Asin(Bx+c)-d \\ \text{where A is the amplitude} \\ Period=(2\pi)/(B) \\ c\text{ is the phase shift} \\ \text{d is the vertical shift} \end{gathered}`

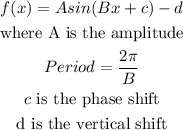
STEP 2: Write the given values

`\begin{gathered} midline=(0,-6) \\ minimum=(2.5,-9) \end{gathered}`

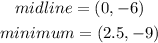
STEP 3: find the amplitude

`\begin{gathered} A=absolute\text{ }difference\text{ between the y-values of the minimum point and the midline} \\ A=|-9-(-6)|=|-9+6|=|-3|=3 \end{gathered}`

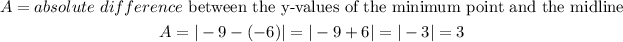
STEP 4: Get the value of B

`\begin{gathered} Period=4*2.5=10 \\ B=(2\pi)/(10)=(\pi)/(5) \end{gathered}`

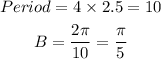
STEP 5: Find the value of c

The function was shifted by 5 units to the right, hence, the value of c is -5

STEP 6: Find the value of the Vertical shift

It can be seen from the midline that the function was shifted by 6 units downwards, therefore, d =6.

STEP 7: Get the sinusoidal function by joining these terms

Hence, the sinusoidal function is given by:

`f(x)=3\sin((\pi)/(5)(x-5))-6`
`f(x)=3\sin((\pi)/(5)(x-5))-6`

`f(x)=3\sin((\pi)/(5)(x-5))-6`