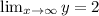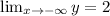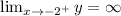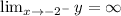Question

Can you please help me with the limits I need help with the graph also. The asymptotes need dotted lines

Answer 1

Given:

`y=(2x^2-5x+2)/(x^2-4)`

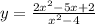
The vertical asymptotes, x= -2

The horizontal asymptotes y=2.

Aim:

We need to graph the function and find the end behavior.

Step-by-step explanation:

The graph of the function:

x-intercept is (0.5,0) and y-intercept is (0, -0.5)

End behavior:

Take the limit of the function:

`\lim _(x\to\infty)y=\lim _(x\to\infty)(2x^2-5x+2)/(x^2-4)`

`\lim _(x\to\infty)y=\lim _(x\to\infty)\frac{2-(5)/(x)+(2)/(x^2)}{1^{}-(4)/(x^2)}`

`\lim _(x\to\infty)y=\frac{2-0+0}{1^{}-0}=2`

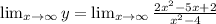
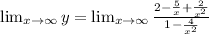
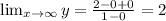
We get

`\lim _(x\to\infty)y=2\text{ }`

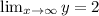
Taking the limit to negative infinity

`\lim _(x\to-\infty)y=\lim _(x\to-\infty)(2x^2-5x+2)/(x^2-4)`

`\lim _(x\to-\infty)y=\frac{2-0+0}{1^{}-0}=2`

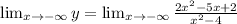
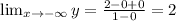
We get

`\lim _(x\to-\infty)y=2\text{ }`

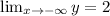
Taking the limit to -2.

`\lim _(x\to-2^+)y=\lim _(x\to-2^+)(2x^2-5x+2)/(x^2-4)`

`\lim _(x\to-2^+)y=\frac{2(-2)^2-5(-2)+2}{(-2)^2_{}-4}=(20)/(0)=\infty`

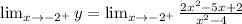
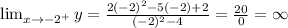
We get

`\lim _(x\to-2^+)y=\infty`

`\lim _(x\to-2^-)y=\lim _(x\to-2^-)(2x^2-5x+2)/(x^2-4)`

`\lim _(x\to-2^-)y=\frac{2(-2)^2-5(-2)+2}{(-2)^2_{}-4}=(20)/(0)=\infty`

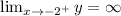
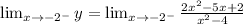
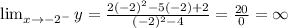
We get

`\lim _(x\to-2^-)y=\infty`

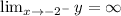
Final answer:

All limits:

`\lim _(x\to\infty)y=2\text{ }`

`\lim _(x\to-\infty)y=2\text{ }`

`\lim _(x\to-2^+)y=\infty`

`\lim _(x\to-2^-)y=\infty`