Answer:
Given that,
we have 200 feet of fencing to enclose a rectangular plot.
Let l be the length of the rectangular plot and x be its width.
we get the quation as,
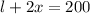
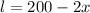
Area of the plot is,
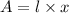
Substitute l in the above equation we get,
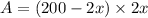
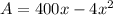
To find the maximum area of the plot,
Differentiating the above equation we get,
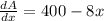
Consider dA/dx =0,
we get,
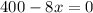
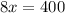
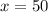
Substitute x in l we get,
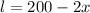
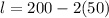
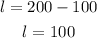
we get,
The width labeled x in the figure is 50 feet.
Answer is: The width labeled x in the figure is 50 feet.
Length of the rectangular plot is 100 feet.
To find the largest area that can be enclosed.
we have that,
Length of the plot is 100 feet
Width of the plot is 50 feet
Area is,
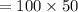
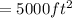
Answer is: Largest area is 5000 square feet.