Step 1: Problem
Area of a rectangle.
Step 2: Concept
Area of a rectangle = Length x width
Draw the diagram with a label.
Step 3: Method
Area of original rectangle = Length x width
= x(x + 6)
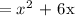
Find the area of the new ractangle.
Area = Length x width
= (x + 10)(x + 4)
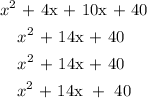
New area - Original area = 104

Step 4: Final answer
Area of the original figure = x(x + 6)
= 8(8 + 6)
= 8 x 14
= 112 in square