We are given the following equation:
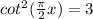
To solve for "x" we will take the square root to both sides:
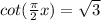
Now, we take the inverse function of cotangent:
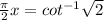
Solving the operations:
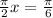
Now, we can cancel out the pi:
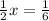
Now, we multiply both sides by 2:
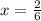
Simplifying:
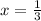
Therefore, the value of "x" is 1/3