Question 4:
The equation of the line:
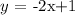
If the point (3, -5) lies on the line, when we substitute the x-value into the equation, we should have the given y-value.
Hence,
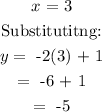
We can conclude that the point (3, -5) lies on the line.
Question 5
Given expression:
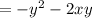
Where:
x = -5 and y = 3:
Substituting we have:
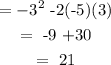
Answer: 21