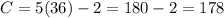Question

This basketball season, Manuel scored 9 less points than Skyler, Dylan scored twice as many points asSkyler, and Corey scored 2 less than 5 times as many points as Skyler. If all 4 players scored a total of313 points this season, how many points did each player score?Number of points scored by Skyler:Number of points scored by Manuel:Number of points scored by Dylan:Number of points scored by Corey:

Answer 1

Let us denote the points scored by each of them as follows:

Manuel = M

Skyler = S

Corey = C

Dylan = D

The information in the question can be "translate" into the language of algebra; it's encoding a linear system of equations:

`\begin{cases}M=S-9 \\ D=2S \\ C=5S-2 \\ M+D+C+S=313\end{cases}`

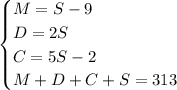
Usually, we use a method for solving this kind of system, but here, there is a trick: Let us add the first three equations up; this gives us

`M+D+C=(S-9)+2S+(5S-2)`

Playing a little with the right-hand side, we get

`M+D+C=8S-11`

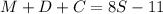
Now, let's play a little with the last equation in the system to get

`M+D+C=313-S`

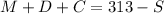
Matching both equations

`8S-11=313-S`

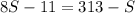
It's an equation with only one variable. We know how to solve it:

`8S+S=313+11`
`9S=324`
`S=(324)/(9)=36`

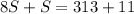
We've not finished yet. We need to find M, D, and C.

M) Replacing the value S=36 in the first equation, we get

`M=36-9=27`

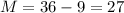
D) Replacing the value S=36 in the second equation, we get

`D=2(36)=72`

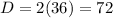
C) Replacing the value S=36 in the third equation, we get

`C=5(36)-2=180-2=178`