Question

Suppose the half- life of a certain radioactive substance is 12 days and there are 18 grams present initially. Find the time when there will be 20% of the initial substance remaining.

Answer 1

27.86 days

Explanation:

The amount, A(t) of a radioactive substance left after time t is modeled by the equation below:

`A(t)=A_o\mleft((1)/(2)\mright)^{(t)/(t_((0.5)))}`

Given:

• Initial Substance, Ao = 18 grams

,

• Half-Life, t(0.5) = 12 days

,

• Amount, A(t)=20% of 18 grams

Substitute into the formula above:

`\begin{gathered} 20\%\text{ of 18}=18_{}\mleft((1)/(2)\mright)^{(t)/(12)} \\ 0.2*18=18\mleft((1)/(2)\mright)^{(t)/(12)} \\ 3.6=18\mleft((1)/(2)\mright)^{(t)/(12)} \end{gathered}`

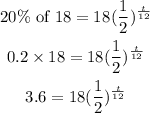
We solve the equation for t below.

`\begin{gathered} \text{Divide both sides by 18} \\ (3.6)/(18)=\frac{18((1)/(2))^{(t)/(12)}}{18} \\ 0.2=\mleft((1)/(2)\mright)^{(t)/(12)} \\ \text{Take the logarithm of both sides} \\ \log (0.2)=\log \mleft((1)/(2)\mright)^{(t)/(12)} \\ \implies(t)/(12)\log (0.5)=\log (0.2) \\ \text{Divide both sides by log(0.5)} \\ (t)/(12)=(\log(0.2))/(\log(0.5)) \\ \text{Multiply both sides by 12} \\ t=12*(\log(0.2))/(\log(0.5)) \\ t=27.86\text{ days} \end{gathered}`

After 27,86 days, there will be 20% of the initial substance remaining.