Answer:
C. x = 8 only
Explanation:
Given the quadratic equation:
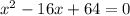
To solve for , we facotorize.
Step 1: Multiply the coefficient of x² and the constant.
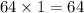
Step 2: Find two numbers that multiply to give 64, and add to give the coefficient of x, -16.
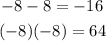
Step 3: Rewrite the middle with those numbers.
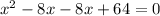
Step 4: Factor the first two and last two terms separately.
Ensure that the expression in the brackets is the same.
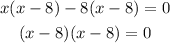
Step 5: Solve for x
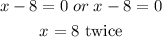
The solution(s) to x² – 16x+64 = 0 is x = 8 only.
Option C is correct.