1 Answer

Prassee · Answer 1 · 2023-08-15T07:50:13+0000

Given

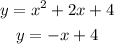
$\begin{gathered} y=x^2+2x+4 \\ y=-x+4 \end{gathered}$

To find the largest value of y in the solution set.

Step-by-step explanation:

It is given that,

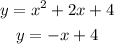
$\begin{gathered} y=x^2+2x+4 \\ y=-x+4 \end{gathered}$

Then,

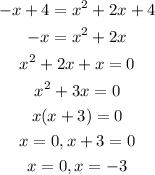
$\begin{gathered} -x+4=x^2+2x+4 \\ -x=x^2+2x \\ x^2+2x+x=0 \\ x^2+3x=0 \\ x(x+3)=0 \\ x=0,x+3=0 \\ x=0,x=-3 \end{gathered}$

Therefore, the solution set is {-3,0}.

That implies, the value of y in the solution set of the system is,

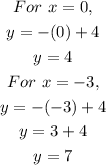
$\begin{gathered} For\text{ }x=0, \\ y=-(0)+4 \\ y=4 \\ For\text{ }x=-3, \\ y=-(-3)+4 \\ y=3+4 \\ y=7 \end{gathered}$

Hence, the largest value of y in the solution set of the system is option d) 7.

Please log in or register to add a comment.