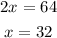For this problem we use two concepts and one fact:
1) The angles opposed by the vertex have the same measure
2) Supplementary angles add up 180 degrees, and
3) The interior angles of a triangle add up 180 degrees.
To find y we notice that the angle of measure (y-8) degrees and the angle of measure 124 degrees are supplementary, therefore:

To find x we use the fact that 2x degrees angle is opposed by the vertex with one interior angle of the triangle.
On the other hand, one of the interior angles of the triangle is opposed by the vertex with the 60 degrees angle, therefore both angles have the same measure. We also know from the previous point that the other interior angle is y-8 degrees= 56 degrees.
Finally, we use that:
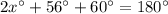
and solving for x we get: