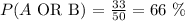Question

A survey of athletes at a high school is conducted, a d the following facts are discovered.63% of the athletes are football players, 34% are basketball players, and 31% of the athletes playboth football and basketball.An athlete is chosen at random from the high school: what is the probability that the athlete iseither a football player or a basketball player?Probability =% (Please enter your answer as a percent)CalculatorScratchwork Area

Answer 1

The probability of choosing an athlete that plays either Basketball or Football is:

`P(A\text{ OR B) = }(33)/(50)=66\text{ \%}`

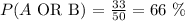
SOLUTION

Problem Statement

The question tells us that a survey revealed that 63% of athletes are footballers, 34% are basketball players while 31% can play both sports.

We are required to find the probability that a randomly chosen athlete can play either basketball or football.

Method

The probabilities of playing basketball and football have been given. Let us take these as two separate events A and B.

We are being asked to find the probability of playing basketball or football; that is, the probability of getting event A or event B.

This question is clearly asking for the OR probability of events A and B, which is given by the formula below:

`P(A\text{ OR B) = P(A) + P(B) - }P(A\cap B)`

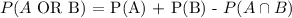
Implementation

To solve the question, we just simply use the formula above. This is done as follows:

1 . First, we shall list out our variables:

`\begin{gathered} \text{If A = Event that the chosen athlete is a footballer} \\ B=Event\text{ that the chosen athlete plays basketball} \\ \\ P(A)=63\text{ \% = }(63)/(100) \\ \\ P(B)=34\text{ \% = }(34)/(100) \\ \\ P(A\cap B)=31\text{ \% = }(31)/(100) \end{gathered}`

2. Apply the formula:

`\begin{gathered} P(A\text{ OR B) = P(A) + P(B) - }P(A\cap B) \\ P(A\text{ OR B) = }(63)/(100)+(34)/(100)-(31)/(100)=(63+34-31)/(100) \\ \\ \therefore P(A\text{ OR B) = }(66)/(100)=(33)/(50) \end{gathered}`

Final Answer

The probability of choosing an athlete that plays either Basketball or Football is:

`P(A\text{ OR B) = }(33)/(50)=66\text{ \%}`